What's Bigger 1/4 Or 1/8? Size Comparison
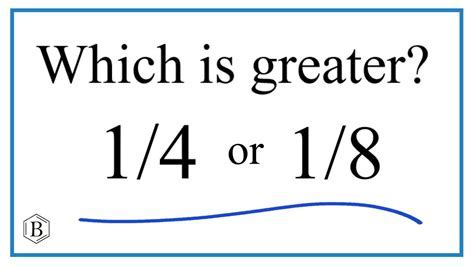
When comparing fractions, it’s essential to understand that the larger the denominator, the smaller the fraction. In this case, we’re comparing 1⁄4 and 1⁄8. To determine which one is bigger, let’s break it down:
1⁄4 can be thought of as dividing a whole into four equal parts and taking one of those parts. Imagine a pizza cut into four slices; if you take one slice, you have 1⁄4 of the pizza.
1⁄8, on the other hand, is dividing a whole into eight equal parts and taking one of those parts. Using the same pizza analogy, if the pizza is cut into eight slices and you take one slice, you have 1⁄8 of the pizza.
Since 1⁄4 represents one out of four parts, and 1⁄8 represents one out of eight parts, 1⁄4 is larger because it represents a larger portion of the whole. To illustrate this further, consider that if you have 1⁄4 of something, you could divide that 1⁄4 into two parts to get two 1/8s. This shows that 1⁄4 is twice as large as 1⁄8.
To make this comparison even clearer, let’s look at a simple visual representation:
- 1⁄4 = 2⁄8 (because 1⁄4 is equivalent to two 1/8s)
- 1⁄8 = 1⁄8
So, when comparing 1⁄4 and 1⁄8, 1⁄4 is bigger because it represents a larger fraction of a whole.
Understanding Fraction Comparisons
When comparing fractions, remember: - The larger the denominator (the number on the bottom), the smaller the fraction. - If the denominators are the same, the fraction with the larger numerator (the number on top) is larger. - To compare fractions with different denominators, convert them to equivalent fractions with the same denominator.
Practical Applications
Understanding fraction comparisons is crucial in various real-world applications, such as cooking, construction, and finance. For instance, when following a recipe, you might need to compare and adjust ingredient ratios, which involves understanding fraction comparisons. In construction, architects and builders must often compare and calculate fractions of measurements to ensure precise fitting and building standards.
Conclusion
In conclusion, when comparing 1⁄4 and 1⁄8, 1⁄4 is indeed bigger. This basic understanding of fraction comparisons is fundamental in mathematics and has numerous practical applications across different fields. By grasping how fractions work and how to compare them, you’ll be better equipped to handle a wide range of problems and tasks, from simple arithmetic to complex calculations and real-world applications.
How do you compare fractions with different denominators?
+To compare fractions with different denominators, you first need to find a common denominator. This can be done by identifying the least common multiple (LCM) of the two denominators and then converting each fraction so that their denominators are the same. Once the denominators are the same, the fraction with the larger numerator is the larger fraction.
Can you give an example of comparing fractions in real life?
+A common real-life example of comparing fractions is in cooking. Let's say a recipe for a cake calls for 3/4 cup of sugar, but you only have a 1/8 cup measuring spoon. To measure out 3/4 cup using the 1/8 cup spoon, you first convert 3/4 into an equivalent fraction with the denominator of 8 (since 4*2=8), which is 6/8. Then, you can use the 1/8 cup spoon six times to get 6/8 or 3/4 cup of sugar.
Incorporating these strategies and examples into your understanding of fraction comparisons will enhance your ability to solve problems not just in mathematics but in everyday situations where fractions are used. Whether you’re cooking a meal, measuring ingredients, or handling financial transactions, knowing how to compare fractions can make a significant difference in accuracy and efficiency.
