What Is Spring Constant? Calculated Easily

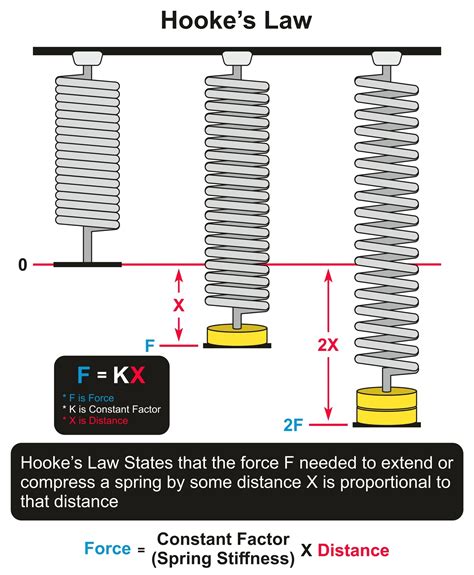
The spring constant, often denoted by the symbol ‘k’, is a fundamental concept in physics that characterizes the stiffness or rigidity of a spring. It is defined as the force required to stretch or compress a spring by a unit distance. In simpler terms, the spring constant is a measure of how much force is needed to cause a certain amount of displacement in a spring. This concept is crucial in understanding and calculating the behavior of springs in various mechanical systems.

To calculate the spring constant, you can use Hooke’s Law, which states that the force (F) exerted on a spring is directly proportional to its displacement (x) from its equilibrium position. Mathematically, this is represented as F = kx, where ‘k’ is the spring constant. By rearranging this formula, you can solve for ‘k’ as k = F/x. This means that if you know the force applied to a spring and the resulting displacement, you can easily calculate the spring constant.

For instance, if a force of 10 Newtons stretches a spring by 2 meters, the spring constant ‘k’ would be calculated as k = 10 N / 2 m = 5 N/m. This result tells you that it takes 5 Newtons of force to stretch or compress this particular spring by 1 meter.

Understanding and calculating the spring constant is not only important for designing and analyzing mechanical systems but also for predicting how objects will behave under different forces and conditions. Whether you’re an engineer designing a new suspension system for a vehicle or a physicist studying the vibrations of molecules, the spring constant is a critical parameter that helps in making accurate predictions and designs.

In real-world applications, the spring constant can vary widely depending on the material and construction of the spring. For example, a spring made from a stiff material like steel will have a higher spring constant compared to one made from a more flexible material like rubber. This difference in spring constants affects how each spring responds to force, making the calculation of the spring constant a crucial step in a wide range of engineering and scientific applications.

Furthermore, the concept of the spring constant extends beyond the physical properties of springs themselves. It can be used as an analogy to understand the behavior of other elastic materials and systems that exhibit similar force-displacement relationships. This broader application of the spring constant concept underscores its importance as a fundamental principle in understanding how materials and systems respond to external forces.

In conclusion, the spring constant is a vital parameter that characterizes the elastic properties of springs and other materials. Its calculation, based on the straightforward principle of Hooke’s Law, provides valuable insights into the mechanical behavior of systems. Whether in the context of spring design, materials science, or broader mechanical analyses, understanding and accurately calculating the spring constant is essential for making informed decisions and predictions in a wide array of scientific and engineering contexts.

Practical Applications of Spring Constant

The spring constant has numerous practical applications across various fields, including engineering, physics, and materials science. Here are a few examples:

1. Design of Mechanical Systems: In the design of mechanical systems such as car suspensions, engine mounts, and vibration isolators, the spring constant is crucial. It helps engineers to balance the stiffness of the system with the need to absorb shocks and vibrations, ensuring both stability and comfort.

2. Materials Science: The spring constant is used to characterize the elastic properties of materials. By measuring how different materials respond to force, scientists can understand their potential applications and limitations.

3. Vibration Analysis: In the analysis of vibrating systems, the spring constant is essential for predicting how a system will respond to different frequencies of vibration. This is critical in the design of structures and machines that are subject to vibrational stresses.

4. Biomechanics: Even in the field of biomechanics, the concept of the spring constant can be applied to understand the elastic properties of biological tissues and systems. For example, understanding the spring constant of tendons and ligaments can provide insights into their function and potential for injury.

Enhanced Understanding through Analogies

To deepen the understanding of the spring constant and its applications, analogies can be quite helpful. For instance, consider a trampoline. The trampoline’s surface can be thought of as a large, flexible spring. When you jump on it, you exert a force that displaces the surface downwards. The stiffer the trampoline (or the higher its spring constant), the less it will deform under your weight, and the more force you will need to apply to achieve a certain displacement. This analogy can help in visualizing how the spring constant affects the behavior of elastic systems.

Mathematical Formulation

Mathematically, the behavior of a spring can be described by Hooke’s Law, as mentioned earlier: F = kx. However, in real-world applications, springs are often subjected to more complex conditions, such as variable forces, damping (the dissipation of energy), and external vibrations. To account for these factors, more advanced mathematical models are used, such as the mass-spring-damper system, which can be represented by the equation: m*x” + c*x’ + k*x = F(t), where m is the mass, c is the damping coefficient, k is the spring constant, x is the displacement, and F(t) is the external force as a function of time. This equation provides a more comprehensive understanding of how springs and similar elastic systems behave under a variety of conditions.

Conclusion on Spring Constant Calculations

In conclusion, calculating the spring constant is a straightforward process that involves understanding the fundamental relationship between force and displacement in elastic systems. Whether you’re dealing with the design of mechanical systems, the analysis of materials, or the prediction of vibrational behavior, the spring constant is a critical parameter. By applying Hooke’s Law and considering the practical applications and analogies, one can gain a deep understanding of the spring constant and its role in characterizing the elastic properties of springs and other materials.