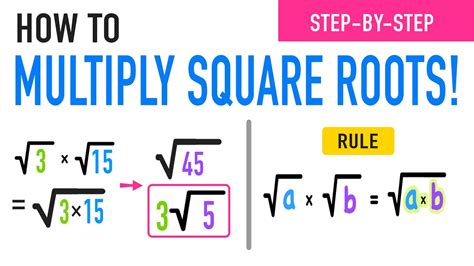
Multiplying by a square root can seem like a complex operation, but it’s actually quite straightforward once you understand the basics. In essence, multiplying by a square root involves using the properties of radicals to simplify the expression. To start, let’s break down what multiplying by a square root entails and how to approach it with simple steps.
Understanding Square Roots
Before diving into multiplication, it’s crucial to understand what a square root is. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 multiplied by 4 equals 16.
Multiplying by a Square Root: Simplified Steps
Identify the Radical Expression: First, identify the square root (radical) in your multiplication problem. This could be something like √16 or √x, where ‘x’ is a variable.
Simplify the Radical (if possible): If the number under the square root is a perfect square (like 16, 25, 36, etc.), simplify it. For instance, √16 simplifies to 4 because 4^2 = 16.
Multiply Outside the Radical: If you’re multiplying a number by a square root (e.g., 3 * √16), first simplify the radical if possible (as in step 2). Then, multiply the number by the simplified radical. In this case, since √16 = 4, you multiply 3 by 4, resulting in 12.
Multiply Variables with Radicals: When multiplying variables with radicals (like x * √y), you keep the variable as is and multiply it by the radical. For example, if you have x * √4, you simplify √4 to 2 and then have x * 2 = 2x.
Multiplying Two Radicals: When multiplying two square roots (like √a * √b), you multiply what’s inside the radicals together and keep the result under a single radical sign. For instance, √a * √b = √(a*b).
Apply to Complex Problems: For more complex problems, like multiplying an expression with multiple terms by a square root (e.g., (2x + 3) * √4), you distribute the multiplication across each term in the expression. Simplify the radical (√4 = 2), then distribute: (2x + 3) * 2 = 4x + 6.
Examples for Clarity
- Simple Multiplication: 5 * √9 = 5 * 3 (since √9 = 3) = 15.
- Variable Multiplication: x * √16 = x * 4 = 4x.
- Radical to Radical: √4 * √9 = √(4*9) = √36 = 6.
- Expression Multiplication: (3x + 2) * √4 = (3x + 2) * 2 = 6x + 4.
Conclusion
Multiplying by a square root involves understanding the properties of radicals and applying them to simplify expressions. By following these simplified steps, you can tackle a range of multiplication problems involving square roots, from simple numerical values to more complex expressions with variables. Remember, the key is to simplify radicals when possible and then perform the multiplication as you normally would, keeping track of any variables or constants involved.
