Solving A Double Integral

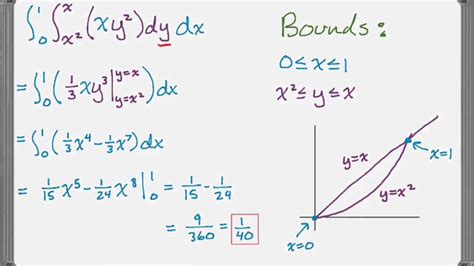
The process of solving a double integral is a fundamental concept in calculus, allowing us to find the volume under a surface in three-dimensional space or the area of a region in the plane when the region’s boundary is not easily expressed as a function of one variable. This technique is crucial in various fields such as physics, engineering, and economics for problems involving optimization, centers of mass, and moments of inertia.

To begin with, consider a double integral of the form \int_{x=a}^{x=b} \int_{y=g(x)}^{y=h(x)} f(x,y) \,dy\,dx, where f(x,y) is a function of two variables, and the limits of integration for y are functions of x. This represents integrating f(x,y) over a region R in the xy-plane bounded by the curves y=g(x) and y=h(x), and the lines x=a and x=b.

Step 1: Define the Region of Integration

The first step in solving a double integral is to clearly define the region of integration. This involves understanding the boundaries of the region, which could be defined by functions of x, functions of y, or a combination of both. For instance, the region might be bounded by y = x^2, y = 2x, x = 0, and x = 3. It’s essential to sketch the region to visualize how the limits of integration will be determined.

Step 2: Determine the Limits of Integration

After defining the region, the next step is to determine the limits of integration for both x and y. The limits for y are often functions of x because we integrate with respect to y first. In the given example, y ranges from x^2 to 2x for any given x. The limits for x are the values that bound the region in the x-direction. In our example, x ranges from 0 to 3.

Step 3: Set Up the Double Integral

With the limits of integration determined, the next step is to set up the double integral. The general form is \int_{a}^{b} \int_{g(x)}^{h(x)} f(x,y) \,dy\,dx. Substituting the limits and the function f(x,y) into this form gives us the specific integral to solve.

Step 4: Evaluate the Inner Integral

To solve the double integral, we first integrate with respect to y, treating x as a constant. This means we integrate f(x,y) from y=g(x) to y=h(x), which gives us a function of x. After evaluating the inner integral, we obtain an expression in terms of x.

Step 5: Evaluate the Outer Integral

Next, we integrate the result from Step 4 with respect to x, from x=a to x=b. This step involves integrating the function obtained after the inner integration, which results in a numerical value.

Example: Solving a Double Integral

Consider the double integral \int_{0}^{3} \int_{x^2}^{2x} (x+y) \,dy\,dx.

• Step 1 & 2: The region R is bounded by y=x^2, y=2x, x=0, and x=3.
• Step 3: The integral is set up as \int_{0}^{3} \int_{x^2}^{2x} (x+y) \,dy\,dx.
• Step 4: Evaluating the inner integral first, we treat x as a constant: [ \int{x^2}^{2x} (x+y) \,dy = \left[xy + \frac{y^2}{2}\right]{x^2}^{2x} = \left(x(2x) + \frac{(2x)^2}{2}\right) - \left(x(x^2) + \frac{(x^2)^2}{2}\right) ] Simplifying, we get: [ = 2x^2 + 2x^2 - x^3 - \frac{x^4}{2} = 4x^2 - x^3 - \frac{x^4}{2} ]
• Step 5: Now, integrate this result with respect to x from 0 to 3: [ \int{0}^{3} \left(4x^2 - x^3 - \frac{x^4}{2}\right) \,dx = \left[\frac{4x^3}{3} - \frac{x^4}{4} - \frac{x^5}{10}\right]{0}^{3} ] Evaluating this from 0 to 3: [ = \left(\frac{4(3)^3}{3} - \frac{(3)^4}{4} - \frac{(3)^5}{10}\right) - 0 = 36 - \frac{81}{4} - \frac{243}{10} ] Simplifying further gives the final numerical answer.

Tricks for Evaluating Double Integrals

• Change of Variables: Sometimes, a change of variables can simplify the integral. This is particularly useful for regions that are not easily expressed in Cartesian coordinates.
• Polar Coordinates: For regions involving circles or sectors, converting to polar coordinates can significantly simplify the evaluation of the double integral.
• Iterated Integration: Being able to integrate in both orders (dy dx or dx dy) is crucial, as some problems may be more straightforward in one order than the other.

Common Mistakes and Challenges

• Incorrect Limits: One of the most common mistakes is setting incorrect limits of integration. It’s crucial to meticulously define the region and determine the limits for both x and y.
• Integration Order: Another challenge is deciding the order of integration. The choice can affect the ease of solving the integral and should be chosen based on the simplicity of the resulting expressions.

Conclusion

Solving double integrals is a powerful tool in mathematics and its applications, enabling us to calculate volumes, areas, and other quantities in two-dimensional regions and three-dimensional spaces. By carefully defining the region of integration, determining the correct limits, and methodically evaluating the integrals, one can master this complex but rewarding aspect of calculus.