Pressure Loss In Pipe Calculator
Pressure loss in pipes is a critical factor to consider in the design and operation of piping systems, as it directly affects the efficiency and cost of fluid transportation. The pressure loss, also known as head loss, in a pipe is the decrease in pressure from the inlet to the outlet of the pipe due to the frictional resistance to flow. This resistance is caused by the interaction between the fluid and the pipe wall, as well as the fluid’s viscosity and the presence of any obstacles or fittings within the pipe.
To accurately calculate pressure loss in pipes, several factors must be considered, including the pipe’s diameter, length, and material, the fluid’s properties such as density and viscosity, and the flow rate. The most commonly used method for calculating pressure loss is the Darcy-Weisbach equation, which is given by:
h = (f * L * v^2) / (2 * g * D)
where: - h is the head loss (in meters), - f is the Darcy friction factor (dimensionless), - L is the length of the pipe (in meters), - v is the average flow velocity (in meters per second), - g is the acceleration due to gravity (approximately 9.81 m/s^2), - D is the diameter of the pipe (in meters).
The Darcy friction factor (f) depends on the flow regime (laminar or turbulent) and the pipe’s surface roughness. For laminar flow, f can be calculated using the Hagen-Poiseuille equation, while for turbulent flow, the Colebrook-White equation or the Moody diagram can be used.
Steps to Calculate Pressure Loss
Determine the Flow Regime: Decide whether the flow is laminar or turbulent. This can be done by calculating the Reynolds number (Re), which is given by Re = ρ * v * D / μ, where ρ is the fluid density, v is the average flow velocity, D is the pipe diameter, and μ is the dynamic viscosity of the fluid. If Re < 2000, the flow is laminar; if Re > 4000, the flow is turbulent.
Calculate the Darcy Friction Factor (f): Use the appropriate equation or diagram based on the flow regime. For turbulent flow, the Colebrook-White equation is f = [-2 * log10(ε / (3.7 * D) + 2.51 / (Re * √f))]^(-2), where ε is the pipe’s surface roughness.
Apply the Darcy-Weisbach Equation: Substitute the calculated f, along with the known values of L, v, g, and D, into the Darcy-Weisbach equation to find the head loss h.
Convert Head Loss to Pressure Loss: The head loss (h) in meters of fluid can be converted to pressure loss (ΔP) in Pascals using the formula ΔP = ρ * g * h, where ρ is the fluid density and g is the acceleration due to gravity.
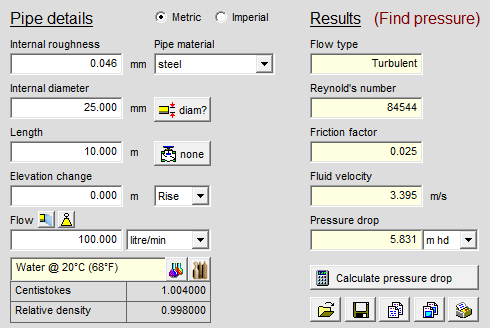
Pressure Loss Calculator
To simplify the calculation process, a pressure loss calculator can be used. These calculators typically require input of the pipe’s dimensions, the fluid’s properties, and the flow conditions. They then use the Darcy-Weisbach equation and the appropriate friction factor correlation to calculate the pressure loss.
Example Input:
- Pipe diameter: 0.1 meters
- Pipe length: 100 meters
- Fluid density: 1000 kg/m^3
- Fluid viscosity: 0.001 Pa·s
- Average flow velocity: 2 m/s
Calculation Steps:
- Determine the Reynolds number to identify the flow regime.
- Calculate the Darcy friction factor based on the flow regime.
- Use the Darcy-Weisbach equation to find the head loss.
- Convert the head loss to pressure loss.
Example Output:
- Reynolds number: 200,000 (turbulent flow)
- Darcy friction factor: 0.018
- Head loss: 12.24 meters
- Pressure loss: 120,249 Pascals or 120.25 kPa
Practical Applications
Understanding and calculating pressure loss is essential for the design and optimization of various systems, including:
- Water Supply Systems: To ensure that water pressure is adequate at all points of consumption.
- Oil and Gas Pipelines: To minimize energy losses and maximize efficiency in long-distance transportation.
- HVAC Systems: To design heating, ventilation, and air conditioning systems that meet the required airflow and pressure specifications.
By accurately calculating pressure loss and considering it in the design phase, engineers can create more efficient, reliable, and cost-effective piping systems.
Conclusion
Calculating pressure loss in pipes is a complex process that involves understanding fluid dynamics, the properties of the fluid and the pipe, and applying the appropriate equations. The Darcy-Weisbach equation, along with the correct friction factor correlation, provides a reliable method for determining pressure loss. Whether using manual calculations or a pressure loss calculator, accurate determination of pressure loss is crucial for the optimal design and operation of piping systems across various industries.
What is the Darcy-Weisbach equation used for?
+The Darcy-Weisbach equation is used to calculate the head loss due to friction in a pipe. It is a fundamental tool in the design of piping systems, allowing engineers to predict pressure drop and ensure that systems operate efficiently.
How do you determine if flow is laminar or turbulent?
+The nature of the flow (laminar or turbulent) is determined by calculating the Reynolds number. If the Reynolds number is less than 2000, the flow is laminar. If it is greater than 4000, the flow is turbulent. Between 2000 and 4000, the flow is in a transitional regime and can be either laminar or turbulent depending on other factors.
What factors affect pressure loss in a pipe?
+Pressure loss in a pipe is affected by several factors, including the pipe's diameter, length, and material, the fluid's density and viscosity, the flow rate, and the presence of fittings or obstacles within the pipe. Each of these factors contributes to the overall resistance to flow, which directly influences the pressure loss.
By understanding these principles and applying them accurately, professionals can design and operate piping systems that meet the required specifications, ensuring efficiency, safety, and reliability. Whether it’s for water supply, oil and gas transportation, or HVAC systems, accurate pressure loss calculation is a critical component of successful system design and operation.


