Inverse Power Function

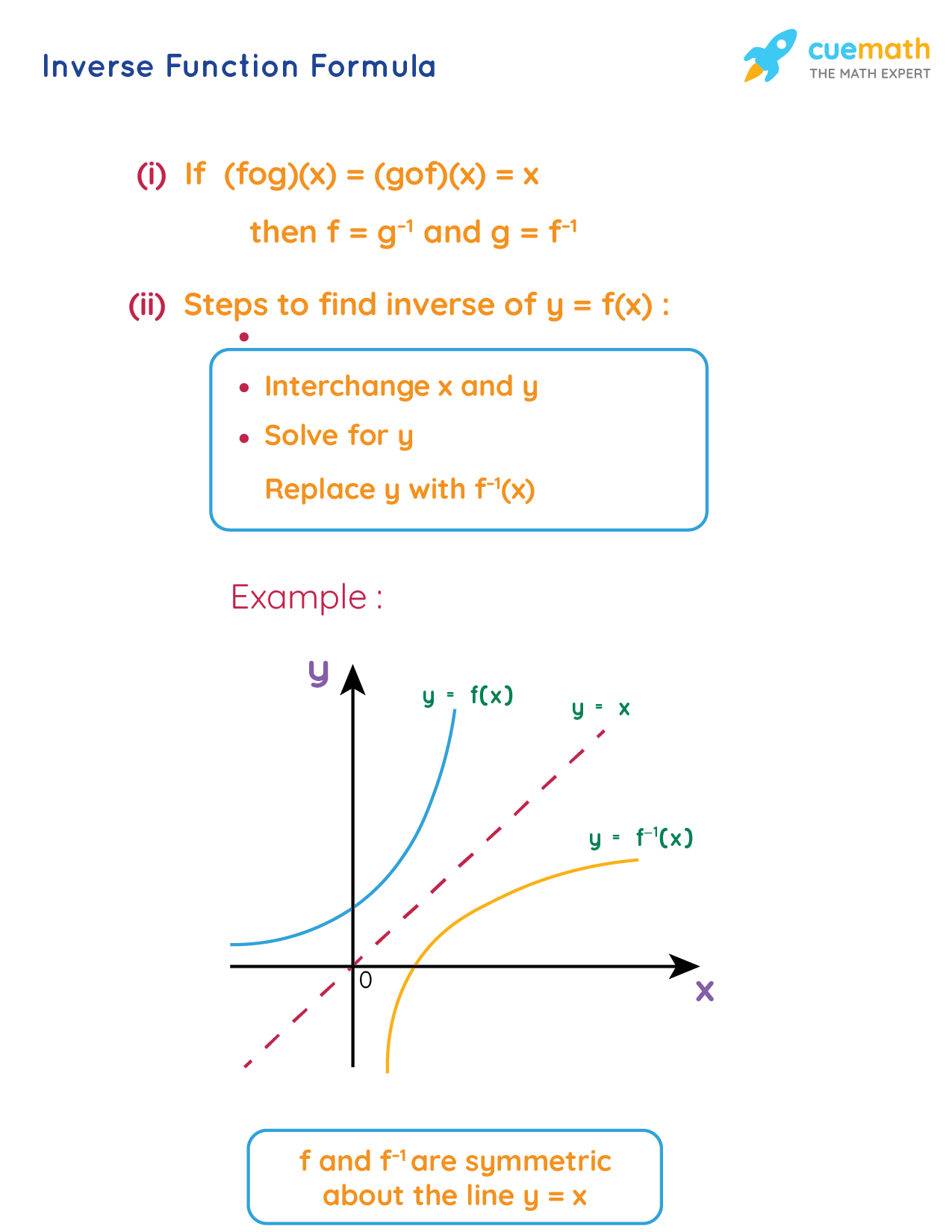
The inverse power function is a mathematical concept that has numerous applications across various fields, including physics, engineering, and economics. At its core, the inverse power function is a relationship between two variables where one variable is inversely proportional to a power of the other variable. This relationship is often represented as (y = \frac{k}{x^n}), where (y) is the dependent variable, (x) is the independent variable, (k) is a constant, and (n) is the power to which (x) is raised.

To delve deeper into the concept, let’s consider a historical evolution of how inverse power functions have been utilized and understood. Historically, the study of inverse power functions traces back to the earliest days of calculus, where mathematicians like Newton and Leibniz laid the groundwork for understanding rates of change and accumulation. The inverse power function, as a specific case, has been particularly useful in modeling real-world phenomena where the effect of one variable on another diminishes as the variable increases.

Problem-Solution Framework: Applications of Inverse Power Functions

One of the primary applications of inverse power functions is in the field of physics, particularly in the study of gravitational forces and electromagnetic forces. According to Newton’s law of universal gravitation, the force between two masses is inversely proportional to the square of the distance between their centers. This can be represented by an inverse power function, where (F = \frac{Gm_1m_2}{r^2}), with (F) being the gravitational force, (G) the gravitational constant, (m_1) and (m_2) the masses of the two objects, and (r) the distance between the centers of the two masses.

Similarly, in economics, the concept of diminishing marginal utility can be modeled using an inverse power function. As the quantity of a commodity consumed increases, the additional satisfaction (marginal utility) derived from each successive unit of the commodity decreases. This relationship can be key in understanding consumer behavior and demand curves.

Comparative Analysis: Inverse Power Functions vs. Other Mathematical Models

When comparing inverse power functions to other mathematical models, such as linear or exponential functions, it becomes apparent that each has its unique advantages and disadvantages. Linear functions are straightforward and easy to analyze but often fail to capture the complexity of real-world relationships. Exponential functions can model rapid growth or decay but may not accurately represent situations where the rate of change decreases over time.

Inverse power functions, on the other hand, offer a balance by providing a flexible model that can capture a wide range of phenomena, from physical forces to economic behaviors. However, they can be more challenging to analyze, especially when the power (n) is not an integer, and may require numerical methods or approximations.

Technical Breakdown: Analyzing Inverse Power Functions

Analyzing an inverse power function involves understanding its behavior as (x) approaches certain critical values, such as zero or infinity. For the function (y = \frac{k}{x^n}), as (x) approaches zero, (y) approaches infinity if (n > 0), demonstrating a vertical asymptote at (x = 0). Conversely, as (x) approaches infinity, (y) approaches zero, showing that the function decreases without bound as (x) increases.

This behavior is crucial in applications like signal processing, where filters based on inverse power functions can be designed to attenuate high frequencies (as the frequency (x) increases, the amplitude (y) decreases), thus smoothing out signals.

Future Trends Projection: Emerging Applications

Looking ahead, the application of inverse power functions is expected to expand into emerging fields like nanotechnology and biophysics. In nanotechnology, understanding the behavior of materials at the nanoscale, where physical properties can significantly deviate from their bulk counterparts, is crucial. Inverse power functions can model the unique scaling laws that govern the behavior of nanostructures, such as their thermal or electrical conductivity.

In biophysics, the interaction between biomolecules, like proteins and DNA, often follows complex patterns that can be described using inverse power functions. For example, the binding affinity between two proteins may decrease as the concentration of one protein increases, a relationship that can be modeled and predicted using inverse power functions.

FAQ Section

Decision Framework: Choosing Inverse Power Functions

When deciding whether to use an inverse power function to model a relationship, consider the following criteria: 1. Nature of the Relationship: Is the relationship between the variables such that one decreases as the other increases, potentially in a non-linear fashion? 2. Presence of Asymptotes: Does the relationship exhibit behavior that can be described by asymptotes, such as vertical or horizontal asymptotes? 3. Scalability: Does the relationship scale in a way that can be captured by an inverse power law, showing diminishing effects as one variable increases? 4. Complexity: Is the relationship complex enough that simpler models (like linear or exponential functions) fail to capture its essence accurately?

By evaluating these factors, one can determine if an inverse power function is an appropriate choice for modeling the relationship in question.

Conclusion

Inverse power functions represent a versatile and powerful tool in the arsenal of mathematical modeling, capable of describing a wide range of phenomena across various disciplines. Their unique properties, such as the presence of asymptotes and the ability to model diminishing effects, make them particularly suited for applications in physics, economics, and emerging technologies. As our understanding of complex systems and phenomena evolves, the role of inverse power functions in capturing and predicting the behavior of these systems will continue to grow, providing valuable insights and solving real-world problems.