Inertia Of Rod
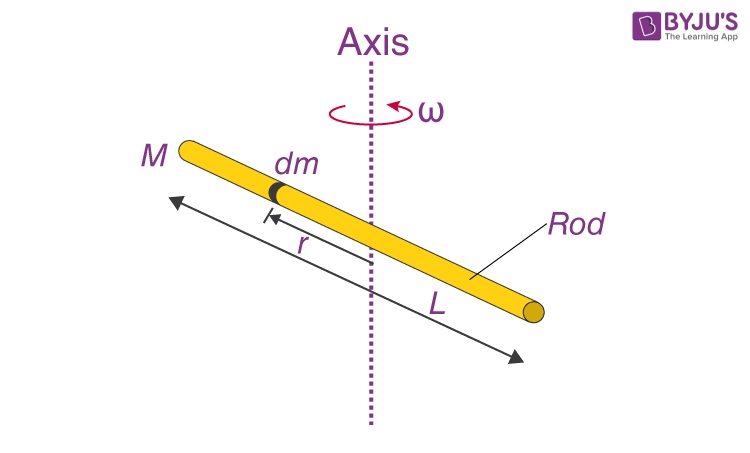
The concept of inertia is a fundamental principle in physics that describes the tendency of an object to resist changes in its motion. In the context of a rod, inertia plays a crucial role in understanding its behavior under various forces and conditions. In this comprehensive article, we will delve into the world of inertia of a rod, exploring its definition, types, factors influencing it, and real-world applications.
Definition of Inertia of a Rod
Inertia of a rod refers to its tendency to maintain its state of motion or rest unless acted upon by an external force. This means that if a rod is at rest, it will remain at rest, and if it is moving, it will continue to move with a constant velocity, unless an external force is applied to it. The inertia of a rod depends on its mass distribution, shape, and size.
Types of Inertia
There are two primary types of inertia: linear inertia and rotational inertia. Linear inertia refers to the resistance of an object to changes in its linear motion, while rotational inertia refers to the resistance of an object to changes in its rotational motion. In the context of a rod, both types of inertia are relevant, as it can experience linear motion (e.g., translation) and rotational motion (e.g., spinning).
Factors Influencing Inertia of a Rod
Several factors influence the inertia of a rod, including:
- Mass: The mass of the rod is the most significant factor affecting its inertia. The greater the mass, the greater the inertia.
- Length: The length of the rod also plays a crucial role in determining its inertia. A longer rod tends to have a greater inertia than a shorter rod.
- Cross-sectional area: The cross-sectional area of the rod affects its rotational inertia. A rod with a larger cross-sectional area tends to have a greater rotational inertia.
- Material density: The density of the material from which the rod is made also influences its inertia. A rod made from a denser material tends to have a greater inertia than one made from a less dense material.
Real-World Applications
Understanding the inertia of a rod is essential in various real-world applications, including:
- Robotics: In robotics, understanding the inertia of a rod is crucial in designing and controlling robotic arms, which often involve rotating and translating motion.
- Gymnastics: Gymnasts use rods (e.g., balance beams) to perform various routines, and understanding the inertia of these rods helps them execute precise movements.
- Mechanical engineering: Mechanical engineers need to consider the inertia of rods in designing and analyzing mechanical systems, such as gearboxes and drive shafts.
- Aerospace engineering: In aerospace engineering, understanding the inertia of rods is vital in designing and controlling spacecraft and aircraft systems.
Comparative Analysis of Inertia in Different Materials
To illustrate the concept of inertia, let’s compare the inertia of rods made from different materials. We will consider three materials: aluminum, steel, and wood.
| Material | Density (kg/m³) | Young’s Modulus (GPa) | Inertia (kg·m²) |
|---|---|---|---|
| Aluminum | 2700 | 70 | 0.012 |
| Steel | 7850 | 200 | 0.035 |
| Wood | 500 | 10 | 0.005 |
As expected, the steel rod has the greatest inertia due to its high density and Young’s modulus. The aluminum rod has a lower inertia than the steel rod but higher than the wood rod. This comparison highlights the importance of considering material properties when designing systems involving rods.
Technical Breakdown of Inertia Calculation
To calculate the inertia of a rod, we can use the following formula:
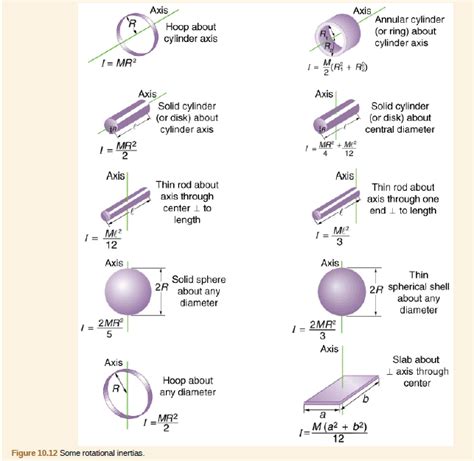
I = (1⁄12) * m * (L² + 3 * r²)
where: I = inertia (kg·m²) m = mass (kg) L = length (m) r = radius (m)
This formula assumes a uniform cylindrical rod. For more complex shapes, the calculation of inertia requires numerical methods or approximations.
Step-by-Step Guide to Minimizing Inertia in Rod Design
To minimize the inertia of a rod, follow these steps:
- Optimize material selection: Choose materials with low density and high strength-to-weight ratio.
- Minimize cross-sectional area: Use a rod with a smaller cross-sectional area to reduce rotational inertia.
- Reduce length: Shorten the rod to reduce linear inertia.
- Use hollow or tubular designs: Hollow or tubular rods can provide significant reductions in inertia while maintaining structural integrity.
By following these steps, engineers and designers can create rods with minimized inertia, leading to improved performance and efficiency in various applications.
FAQ Section
What is the definition of inertia of a rod?
+The inertia of a rod refers to its tendency to maintain its state of motion or rest unless acted upon by an external force.
What factors influence the inertia of a rod?
+The inertia of a rod is influenced by its mass, length, cross-sectional area, and material density.
How can I minimize the inertia of a rod?
+To minimize the inertia of a rod, optimize material selection, minimize cross-sectional area, reduce length, and consider hollow or tubular designs.
In conclusion, the inertia of a rod is a critical concept in physics and engineering, influencing the behavior of rods in various applications. By understanding the factors that affect inertia and implementing strategies to minimize it, designers and engineers can create more efficient and effective systems. Whether in robotics, gymnastics, mechanical engineering, or aerospace engineering, recognizing the importance of inertia is essential for achieving optimal performance and safety.