How To Calculate Moment Of Inertia? Simplified Guide

Calculating the moment of inertia is a fundamental concept in physics and engineering, crucial for understanding the rotational dynamics of objects. The moment of inertia, often denoted by the letter I, is a measure of an object’s resistance to changes in its rotation. It depends on the object’s mass distribution and the axis around which it rotates. In this guide, we will delve into the simplified steps to calculate the moment of inertia for various shapes and discuss its importance in real-world applications.

Understanding the Basics

Before diving into the calculations, it’s essential to understand what the moment of inertia represents. It is a measure of how the mass of an object is distributed around a given axis. The farther the mass is from the axis, the larger the moment of inertia, indicating a greater resistance to rotational acceleration. This concept is analogous to mass in linear motion, where mass represents resistance to linear acceleration.

Formula for Moment of Inertia

The general formula for the moment of inertia is given by:

[I = \int r^2 dm]

Where: - (I) is the moment of inertia, - (r) is the distance of the mass element from the axis of rotation, - (dm) is the mass element.

However, for most standard shapes, there are specific formulas derived from this general equation, eliminating the need for integration.

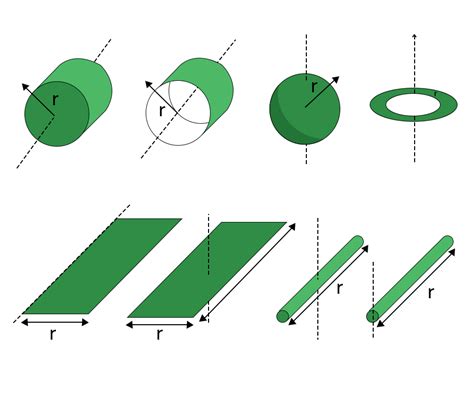
Calculating Moment of Inertia for Common Shapes

1. Point Mass: For a point mass (m) located a distance (r) from the axis of rotation, the moment of inertia is simply (I = mr^2).

2. Solid Sphere: For a solid sphere of mass (m) and radius (r), the moment of inertia about its central axis is (I = \frac{2}{5}mr^2).

3. Hollow Sphere: For a hollow sphere of mass (m) and radius (r), rotating about its central axis, (I = \frac{2}{3}mr^2).

4. Rod: For a rod of length (L) and mass (m), rotating about an axis perpendicular to the rod and through its center, (I = \frac{1}{12}mL^2). If the rotation axis is at one end of the rod, (I = \frac{1}{3}mL^2).

5. Cylinder: For a solid cylinder of mass (m), radius (r), and height (h), rotating about its central axis, (I = \frac{1}{2}mr^2).

6. Rectangular Plate: For a rectangular plate of mass (m), length (a), and width (b), rotating about an axis perpendicular to the plate and through its center, (I = \frac{1}{12}m(a^2 + b^2)).

Step-by-Step Calculation Process

1. Identify the Shape: Determine the shape of the object for which you are calculating the moment of inertia. Ensure it matches one of the standard shapes for which formulas are readily available.

2. Gather Necessary Parameters: Collect the necessary dimensions and mass of the object. This could include radius, length, width, height, or any other parameter relevant to the shape’s moment of inertia formula.

3. Apply the Formula: Select the appropriate formula for the shape of the object and insert the values of the parameters. Perform the calculation to obtain the moment of inertia.

4. Consider the Axis of Rotation: Be sure to consider the axis around which the object is rotating, as this affects the moment of inertia. For some shapes, such as a cylinder or a rod, the moment of inertia can vary significantly depending on the axis of rotation.

Real-World Applications

Understanding and calculating the moment of inertia is crucial in various fields:

• Engineering: In the design of engines, gearboxes, and other rotating machinery, the moment of inertia plays a significant role in determining the rotational kinetics and efficiency of the system.
• Aerospace: The moment of inertia is vital in the design and operation of aircraft and spacecraft, influencing stability, maneuverability, and fuel efficiency.
• Sports Equipment: The moment of inertia affects the performance of sports equipment like golf clubs, tennis rackets, and bicycle wheels, impacting their swing, vibration, and rotational speed.

Conclusion

Calculating the moment of inertia is a straightforward process once you understand the basic concepts and have identified the correct formula for the shape in question. It is a fundamental principle in physics and engineering, essential for the design, analysis, and optimization of rotating systems across various industries. By applying the steps outlined in this guide, you can accurately determine the moment of inertia for a wide range of objects, contributing to a deeper understanding of their rotational dynamics and behavior.

Frequently Asked Questions